FastICA
The goal
Questions to David Rotermund
Test data
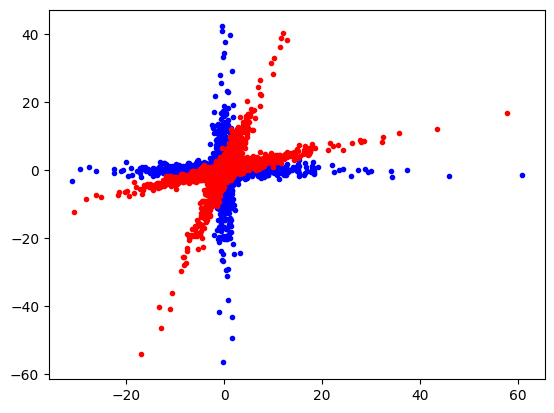
We rotate the blue dots with a non-orthogonal rotation matrix into the red dots.
import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng(1)
a_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
a_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
data_a = np.concatenate((a_x, a_y), axis=1)
b_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
b_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
data_b = np.concatenate((b_x, b_y), axis=1)
data = np.concatenate((data_a, data_b), axis=0)
angle_x = -0.3
angle_y = 0.3
roation_matrix = np.array(
[[np.cos(angle_x), -np.sin(angle_x)], [np.sin(angle_y), np.cos(angle_y)]]
)
data_r = data @ roation_matrix
plt.plot(data[:, 0], data[:, 1], "b.")
plt.plot(data_r[:, 0], data_r[:, 1], "r.")
plt.show()
Train and use FastICA
class sklearn.decomposition.FastICA(n_components=None, *, algorithm='parallel', whiten='unit-variance', fun='logcosh', fun_args=None, max_iter=200, tol=0.0001, w_init=None, whiten_solver='svd', random_state=None)
FastICA: a fast algorithm for Independent Component Analysis.
The implementation is based on 1.
fit(X, y=None)
Fit the model to X.
X : array-like of shape (n_samples, n_features)
Training data, where n_samples is the number of samples and n_features is the number of features.
transform(X, copy=True)
Recover the sources from X (apply the unmixing matrix).
X : array-like of shape (n_samples, n_features)
Data to transform, where n_samples is the number of samples and n_features is the number of features.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FastICA
rng = np.random.default_rng(1)
a_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
a_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
data_a = np.concatenate((a_x, a_y), axis=1)
b_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
b_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
data_b = np.concatenate((b_x, b_y), axis=1)
data = np.concatenate((data_a, data_b), axis=0)
angle_x = -0.3
angle_y = 0.3
roation_matrix = np.array(
[[np.cos(angle_x), -np.sin(angle_x)], [np.sin(angle_y), np.cos(angle_y)]]
)
data_r = data @ roation_matrix
# Train
ica = FastICA(n_components=2)
ica.fit(data_r)
# Use
transformed_data = ica.transform(data_r)
plt.plot(transformed_data[:, 0], transformed_data[:, 1], "k.")
plt.show()
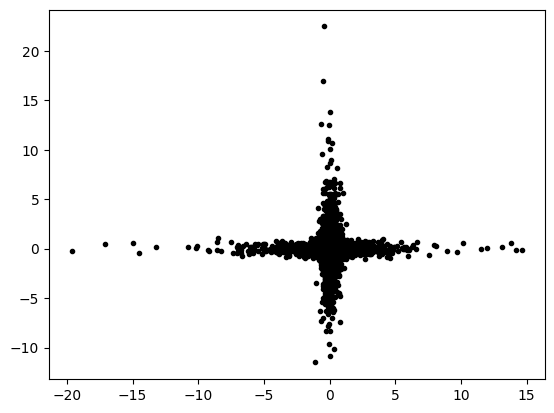
Use FastICA to transform the un-rotated data
inverse_transform(X, copy=True)
Transform the sources back to the mixed data (apply mixing matrix). X : array-like of shape (n_samples, n_components)
Sources, where n_samples is the number of samples and n_components is the number of components.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FastICA
rng = np.random.default_rng(1)
a_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
a_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
data_a = np.concatenate((a_x, a_y), axis=1)
b_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
b_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
data_b = np.concatenate((b_x, b_y), axis=1)
data = np.concatenate((data_a, data_b), axis=0)
angle_x = -0.3
angle_y = 0.3
roation_matrix = np.array(
[[np.cos(angle_x), -np.sin(angle_x)], [np.sin(angle_y), np.cos(angle_y)]]
)
data_r = data @ roation_matrix
# Train
ica = FastICA(n_components=2)
ica.fit(data_r)
# Use
transformed_data = ica.inverse_transform(data)
plt.plot(transformed_data[:, 0], transformed_data[:, 1], "k.")
plt.show()
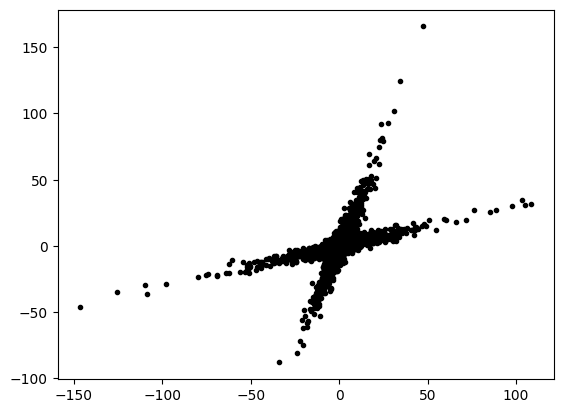
Inspect the extracted coordinate system
components_ : ndarray of shape (n_components, n_features)
The linear operator to apply to the data to get the independent sources. This is equal to the unmixing matrix when whiten is False, and equal to np.dot(unmixing_matrix, self.whitening_) when whiten is True.
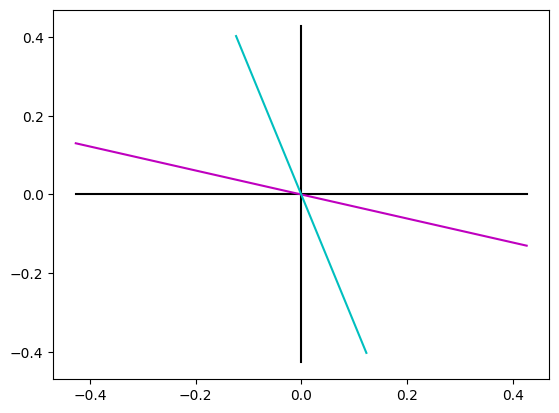
Be aware that the sign of any axis can switch !!! Like it happend in this example:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FastICA
rng = np.random.default_rng(1)
a_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
a_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
data_a = np.concatenate((a_x, a_y), axis=1)
b_x = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis] ** 3
b_y = rng.normal(0.0, 1.0, size=(5000))[:, np.newaxis]
data_b = np.concatenate((b_x, b_y), axis=1)
data = np.concatenate((data_a, data_b), axis=0)
angle_x = -0.3
angle_y = 0.3
roation_matrix = np.array(
[[np.cos(angle_x), -np.sin(angle_x)], [np.sin(angle_y), np.cos(angle_y)]]
)
data_r = data @ roation_matrix
# Train
ica = FastICA(n_components=2)
ica.fit(data_r)
plt.plot([-ica.components_.max(), ica.components_.max()], [0, 0], "k")
plt.plot([0, 0], [-ica.components_.max(), ica.components_.max()], "k")
plt.plot(
[-ica.components_[0, 0], ica.components_[0, 0]],
[-ica.components_[0, 1], ica.components_[0, 1]],
"m",
)
plt.plot(
[-ica.components_[1, 0], ica.components_[1, 0]],
[-ica.components_[1, 1], ica.components_[1, 1]],
"c",
)
plt.show()
Fast ICA Methods
| fit(X[, y]) | Fit the model to X. |
| fit_transform(X[, y]) | Fit the model and recover the sources from X. |
| get_feature_names_out([input_features]) | Get output feature names for transformation. |
| get_metadata_routing() | Get metadata routing of this object. |
| get_params([deep]) | Get parameters for this estimator. |
| inverse_transform(X[, copy]) | Transform the sources back to the mixed data (apply mixing matrix). |
| set_inverse_transform_request(*[, copy]) | Request metadata passed to the inverse_transform method. |
| set_output(*[, transform]) | Set output container. |
| set_params(**params) | Set the parameters of this estimator. |
| set_transform_request(*[, copy]) | Request metadata passed to the transform method. |
| transform(X[, copy]) | Recover the sources from X (apply the unmixing matrix). |
Fast ICA Attributes
components_ : ndarray of shape (n_components, n_features)
The linear operator to apply to the data to get the independent sources. This is equal to the unmixing matrix when whiten is False, and equal to np.dot(unmixing_matrix, self.whitening_) when whiten is True.
mixing_ : ndarray of shape (n_features, n_components)
The pseudo-inverse of components_. It is the linear operator that maps independent sources to the data.
mean_ : ndarray of shape(n_features,)
The mean over features. Only set if self.whiten is True.
n_features_in_ : int
Number of features seen during fit.
feature_names_in_ : ndarray of shape (n_features_in_,)
Names of features seen during fit. Defined only when X has feature names that are all strings.
n_iter_ : int
If the algorithm is “deflation”, n_iter is the maximum number of iterations run across all components. Else they are just the number of iterations taken to converge.
whitening_ : ndarray of shape (n_components, n_features)
Only set if whiten is ‘True’. This is the pre-whitening matrix that projects data onto the first n_components principal components.
The source code is Open Source and can be found on GitHub.
